

发布时间:2021-05-05
中国人民大学余俊伟教授来我院讲授“模态逻辑的历史与现状”
4月27日上午,在文科楼101教室,中国人民大学余俊伟教授为我院2020级本科生带来了关于模态逻辑的课程,向同学们深入浅出地介绍了“模态逻辑的历史与现状”。郭建萍教授主持。

课程开始,余老师将模态逻辑的内容分为传统与现代两个方面,分别进行讲授。
在传统方面,余老师带领我们首先对模态概念进行了回顾。狭义的模态概念表达真势,分为必然和可能;广义的模态概念表达一种规范或信念。在亚里士多德模态逻辑那里,必然模态命题分为必然肯定和必然否定,可能模态命题有可能肯定和可能否定,它们构成模态对当关系。接着,余老师重点阐述了传统模态逻辑的问题与缺陷,即意义的含混不清和不成体系,因此,呼唤严格语义,建立现代模态逻辑必要且重要。
在现代模态逻辑部分,余老师从现代模态逻辑的起源讲起。在实质蕴涵中总存在着“实质蕴涵怪论”。现代模态逻辑创始人刘易斯没有直接从实质蕴涵入手,而是对联结词“或者”的真值情况进行了思考,以“或者Caesar死了,或者月亮是由新鲜乳酪构成”和“或者Matilda不爱我,或者有人爱我”为例,他认为对“或者”引导的命题进行真假断定时,还有一种意义没有被经典逻辑的“或者”联结词所涵盖,刘易斯借助于现代逻辑形式系统方法,发展了严格蕴含逻辑系统,希望克服实质蕴含怪论。
关于可能世界语义学,莱布尼兹首次提出可能世界的思想,认为世界是可能的事物组合,现实世界是由所有可能事物形成的组合。在可能世界中,不包含逻辑矛盾,逻辑始终是一致的,一个命题是必然的,当且仅当它在一切可能世界中为真;一个命题是可能的,当且仅当它在有的可能世界中是真的。卡尔纳普、欣迪卡、克里普克加以完善,形成了可能世界语义学。在可能世界语义学中,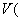
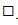
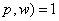 ,
,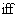 对任一
对任一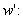
 ,
, ◇
◇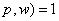 ,
,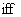 对存在
对存在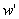 使得
使得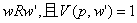 。其中,死点是一种特殊的情况,它不通向任何世界,必然性命题在其中始终为真。框架<W,R>(记为
。其中,死点是一种特殊的情况,它不通向任何世界,必然性命题在其中始终为真。框架<W,R>(记为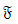 或F)是二元组,W是非空集,R是W上的一个二元关系,在框架中,又分别存在自返的、对称的、传递的和延续的框架。模型<W,R,V>(记为
或F)是二元组,W是非空集,R是W上的一个二元关系,在框架中,又分别存在自返的、对称的、传递的和延续的框架。模型<W,R,V>(记为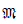 或M),其中<W,R>是一框架,V是一真值指派,给每个命题变元在W中的每个世界(点)指派一真值。在讲解可能世界语义学的过程中,余老师还鼓励我们自己动笔进行计算、进行书写,与我们进行交流和互动。余老师告诫我们,自己动笔也是理解知识的一种方式。
或M),其中<W,R>是一框架,V是一真值指派,给每个命题变元在W中的每个世界(点)指派一真值。在讲解可能世界语义学的过程中,余老师还鼓励我们自己动笔进行计算、进行书写,与我们进行交流和互动。余老师告诫我们,自己动笔也是理解知识的一种方式。

基于此,余老师分析了现代模态逻辑的特征,即严格、清晰且系统化。最后,余老师为我们介绍了当今模态逻辑的研究方向,分别是模态与经典,模态与代数,模态完全性理论和模态形而上学。在模态形而上学的讲解中,余老师向我们抛出了一些问题,如:哲学是本质主义吗?可能与必然的哲学意味什么?

伴随大家对这些问题的思考,余老师为我们讲授的课程也告一段落。进入到提问环节,同学们积极踊跃地提问,余老师对这些问题作了认真细致的回答,解决了同学们在听课过程中存在的一些疑惑。在同学们热烈的掌声中,余老师精彩的课程圆满落幕。
在这短暂而充实的两小时中,余老师带领我们走进模态逻辑,向我们展示了逻辑学中的另一种逻辑系统,丰富了我们逻辑学方面的知识,也加深拓展了我们对逻辑学的认识和理解。


学院订阅号

学院服务号

格致传媒